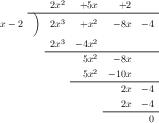
筆算方式
\(A(x)=x^5+x^4–2x^3+x2–3x+1\) を\(B(x)=x^2–x+1\)で割り算したときの商\(Q(x)\)と余り\(R(x)\)を求める.
小学校以来行ってきた多数桁の割り算と同じ方法である.1. 立てる,2.掛ける,3. 引く,4.おろす の 4ステップを繰り返して行うやりかたです.途中で引くでゼロになるか商が1位のくらいまで立ったら終了し引いた結果が余りです.下に\(A(x)\div B(x)\)の例を示しています.商\(Q(x)=x^3+2x^2-x-2\)が最上段に現れている.最下段には余り\(R(x)=-4x+3\)が表示されているのがわかる.
example-crop組み立て除法
組み立て除法は高次式\(A(x)\)を一次式\(B(x)\)で割り算するときに商\Q(x)\)と余り\(R(x)\) とを高次多項式の係数に着目して行う方法である.問題16.(2)を例にしてその方法を説明する.
\(A(x)\)の係数を横に並べて書く,次に\(B(x)=x+a\)として\(-a\)をその右側L字型にところに書く.そうすると\(1 +2 -3 -6\)と\(-3\)が並ぶ.最上位桁(この場合は\(x^3\)の係数\(1\))を下に下ろす(横線の下に書く).次に,この\(1\)と\(-a\)(この場合は\(-3\))と掛けて,その横に書く.次は\(2\)とこの\(-3\)を加算して\(-1\)を下に書く.これを更に行うと,加算の結果が\(0\)になったら終了,もしくは最下位桁まできたら終了する.この例では途中0が出現したところで終了する.これは商の係数を示しており,\(-6\)は余りである.
よって,求める商は\(Q(x)=x^2-x\)で余り\(R(x)=-6\)となる.
fig-kumitate-crop